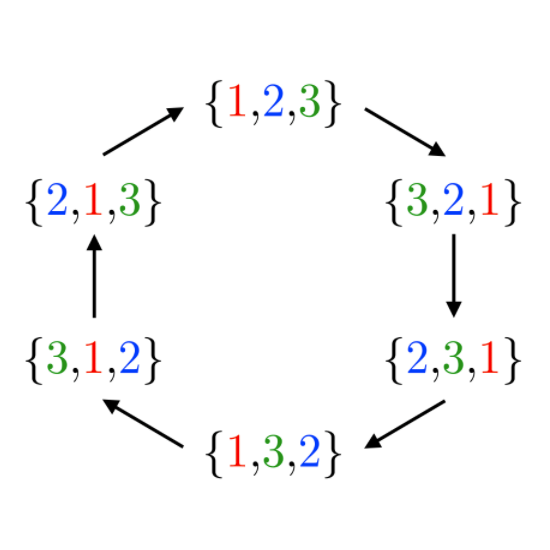
算法原理 相关算法——插入法 对于集合 $$ S=\{a_1, a_2, ..., a_n\} $$ 若已知前 $n-1$ 个元素的全排列，则 $n$ 个元素的全排列 $$ p_i=\{p_1,p_2,...,p_{(n-1)!}\} $$ 可以这样生成：将 $a_n$ 插入 $p_i$ 不同位置中，由此，得到集合 $S$ 的全排列 为什么这样操作能得到集合 $S$ 的全排列？因为每个 $p_i$ 的可能插入位置为 $n$ 个，所以总数是 $n!$ 又因为每个 $p_i$ 是不同的，因此，得到的排列必然没有重复 插入法有一个缺点：为了产生 $n$ 个元素的排列，必须知道并存储所有 $n-1$ 个元素的排列，然后才能产生出所有 $n$ …